Plasma-Turbulenzen im invertierten Magnetron

Ein invertiertes Magnetron ist eine Druckmesszelle, welche im Ultrahochvakuum (UHV) eingesetzt wird. Bei einem Druck von ca. 10e-5 Pa tritt ein Knick in der Druck-Strom Kennlinie auf, welcher bis heute nicht genau erklärt werden kann. Diese Arbeit befasste sich mit der Modellierung des Plasmas und der Untersuchung dieses Knickes. Die Ursachen liegen sehr bei auftretenden Turbulenzen im Plasma, deren Entstehung stark von der Symmetrie des Magnetrons abhängt. Mit Hilfe von Modellen aus Literatur, Messungen und mit diversen Methoden der numerischen wie der analytischen Mathematik wurde versucht, diesen Vorgängen auf die Spur zu kommen. Die Simulation dient hauptsächlich dem Verständnis der auftretenden Effekte, jedoch kann sie auch direkt zur Entwicklung einer verbesserten Messzelle beitragen, indem sie die Entwicklungszeit verkürzt und den aufwendigen Prototypenbau vereinfacht.

Keywords: invertiertes Magnetron, Plasma-Physik, Diocotron-Instabilitäten, Druck-Entladestrom-Kennlinie

Das Magnetron ist eine Kaltkathoden-Druckmesszelle für den Hoch- und Ultrahochvakuumbereich, welches bis zu Drücken von 10-12 mbar eingesetzt werden kann. Durch das Anlegen einer Spannung zwischen Anode und Kathode entsteht ein starles elektrisches Feld. Elektronen werden darin beschleunigt und ioniseren das Restgas. Es entsteht ein Plasma mit Neutralteilchen, Elektronen, ionisierten Gasteilchen und Radikalen. Das invertierte Magnetron besitzt neben einem E-Feld auch noch ein Magnetfeld, welches senkrecht zum E-Feld liegt. Dadurch wird die mittlere freie Weglänge der Elektronen grösser, weil nicht nur die elektrostatische Kraft auf die Elektronen wirkt sondern auch noch eine magnetische Komponente (Lorentz-Kraft), wodurch die Elektronen auf eine Kreisbahn gezwungen werden. Es kommt zu einer ExB-Driftbewegung, was bewirkt, dass die Elektronen häufiger mit neutralen Gasteilchen kollidieren und so die Ionisationsrate zunimmt. Dadurch kann der Einsatzbereich bis in den tiefen UHV-Bereich gewährleistet werden. Jedoch wird beobachtet, dass die Druck-Entladestrom-Kennlinie bei einem Druck von etwa 10-8 mbar einen Knick macht und auch grosse Varianzen zeigt. Woher kommt dieser Knick?

Für die Modellierung des Plasmas wurde in einem ersten Ansatz ein Zwei Flüssigkeitsmodell (Drift-Diffusions-Modell ) eines neutralen Plasmas verwendet. Die in COMSOL® implementierten partiellen Differentialgleichungen berücksichtigen nicht alle vorkommenden Reaktionen im Plasma, stellen jedoch ein erstes Grundgerüst zur Plasmasimulation dar. Im hohen Druckbereich führte dieses Modell zu sehr guten und glaubhaften Resultaten. Im tiefen Druckbereich (UHV) versagt jedoch das Drift-Diffusions-Modell für Elektronen und Ionen. Es bildet sich ein reines nicht-neutrales Elektronen-Plasma aus.

In diesem UHV-Druckbereich könnte mit Hilfe einer Monte Carlo Simulation (MC) das Verhalten der einzelnen Teilchen stochastisch modelliert werden [10]. Eine vollständige MC-Simulation mit Berücksichtigung aller Reaktionsarten hätte den Rahmen der Arbeit gesprengt. Jedoch wurden die Elektron-Trajektorien für diesen Druckbereich sowohl analytisch in MATLAB® wie auch numerisch in COMSOL® berechnet und anschliessend verglichen. Es können sehr unterschiedliche Trajektorien auftreten. Diese hängen sehr stark von den verwendeten Startwerten des Partikels ab. Mit der Berechnung dieser Trajektorien ist der erste Schritt zu einer MC-Simulation getan. Ein vergleich mit dem effektiven Potential der Elektronen im B-Feld zeigt, dass die Aufenthaltswahrscheinlichkeit der Elektronen gut mit dem minimum des effektiven Potentials übereinstimmt [9].

Ein ausführliches Literaturreview zum Thema Magnetron-Knick wurde durchgeführt. Seit der Entdeckung der Ionisationsvakuummesszelle wurde zu diesem Thema sehr viel publiziert [1-7,11-12]. Dennoch ist es bis heute ein ungelöstes Problem geblieben. Schon mehr als 40 Jahre liegt der Verdacht nahe, dass die Ursache in den Diocotron-Oszillationen und daraus entstehenden Instabilitäten (Turbulenzen) liegt. Diese Theorie scheint glaubwürdig. Trotzdem fehlt ein Baustein, um den direkten Zusammenhang zwischen den Instabilitäten und dem Knick in der Kennlinie belegen zu können.

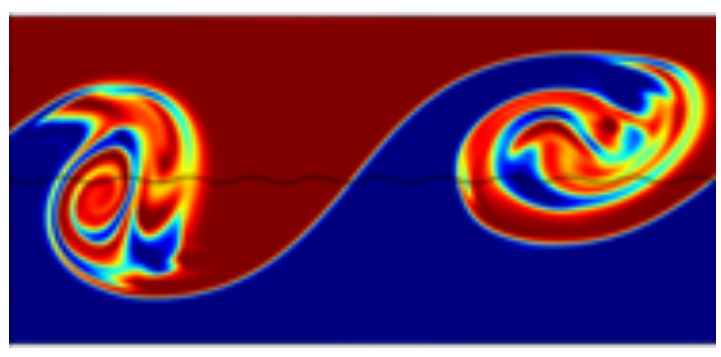
Für ein reines Elektronenplasma (UHV-Bereich) im zylindersymmetrischen Fall kann gezeigt werden, dass die Plasma-Gleichungen isomorph zu den 2D-Euler Gleichungen sind [7]. Daher wurde versucht, die auftretenden Instabilitäten mit Hilfe dieser Gleichungen qualitativ zu modellieren. Das Modell wurde erweitert durch Verwendung der Navier-Stokes Gleichungen zweier Flüssigkeiten. Die auftretenden Kelvin-Helmholtz Instabilitäten sind analog zu den Diocotron Instabilitäten im Plasma. Figur 3 zeigt die Turbulenz zweier Flüssigkeiten, die aneinander reiben. Ähnlich turbulent wird sich die Elektronendichte im Ringstrom des Magnetrons im Bereich des Magnetron-Knicks verhalten. Diese Dichte-Turbulenzen verursachen Instabilitäten im Entladestrom, was experimentell auch nachgewiesen wurde [4,7-8]. Der Knick ist unserer Meinung nach nicht eine definierte Stufe, sondern eher der Übergang von einem stabilen Zustand in einen instabilen, turbulenten Zustand. Auch die Messdaten lassen eher diesen Schluss zu.

Mit dieser Arbeit konnte ein Grundstein für das Verständnis der Plasmaphysik und einiger darin auftretender Phänomene gegeben werden. Die Grenze des verwendeten Ansatzes wurde aufgezeigt. Detailliertere Information zur Klärung der Entstehung des Magnetron-Knicks wären hilfreich. Dazu wäre ein manipulierbarer Messaufbau nötig, bei welchem der Entladestrom und zusätzliche Parameter zeitaufgelöst und breitbandig gemessen werden können. Als Modellklasse für die Modellierung eignen sich in diesem Druckbereich für ein nicht-neutrales Plasma die Gleichungen der Magnetohydrodynamik (MHD). Mit diesen zusätzlichen Experimenten und einem validierten MHD-Modell des Magnetrons wird es möglich sein, die Turbulenzen gezielt zu kontrollieren und somit den Magnetron-Knick bereits bei der Entwicklung der Druckmesszellen in Griff zu bekommen.

Referenzen:

[1] PENNING F.M.: The glow discharge at low pressure between coaxial cylinders in an axial magnetic field, Physica 3, (1936), 873-894

[2] ABOLMASOV N.S.: Physics and engineering of crossed-field discharge devices, Plasma Sources Sci. Techn. Palaiseau France (2012), 035006 (14pp)

[3] SCHUURMAN W.: Investigation of a low pressure penning discharge, Physica 36, FOM Institute voor plasma-fyscia, Rijnhuizen, Jutphaas , NL (1967), 136-160

[4] REDHEAD P.A.: Instabilities in crosses-field discharges at low pressures Vacuum, numbers 8-10, Divison of Physics, Nationl Research Council of Canada, Ottawa Canada (1988), 901-906

[5] KNAUER W.: Mechanism of the Penning Discharge at Low Pressures, J. Appl. Phys. 33(6), (1961), 2093-2099

[6] KNAUER W.: Diocotron instability in plasmas and gas Discharge, Journal of applied physics, volume 7, no. 2, Hughes Research Laboratories, Malibu, Californa (1966), 602-611

[7] DRISCOLL C.F.: FINE K.S.: HUANG X.P.: MITCHELL T.B.: CLUGGISH B.P.: Vortices and Turbulent relaxation in magnetized electron columns, Department of physics and institute for pure and applied physical sciences, University of California at San Diego, La Jolla, 1-10

[8] DRISCOLL C.F.: Observation of an unstable l=1 Diocotron mode on hollow electron column, Physical Review letters, vol. 64, no. 6, University of California at San Diego, La Jolla, California (1990), 601-607

[9] WENDT A.E.: Diss. Dynamics of planar magnetron discharge, University of California at Berkeley, (September 1988), 64-79

[10] BOGAERTS A.; KOLEV I.; BUYLE G.: Reactive Sputter Deposition, Modeling of the Magnetron Discharge, Dissertation, (2008), 66-74

[11] KERVALISHVILI N.: JAVAKHISHVILI J.: KERVALISHVILI G.: The l=1 diocotron instability of nonneutral electron plasma in magnetron geometry with thin cathode, Journal of Georgian Geophysical Society. Issue (B) Physics of Atmosphere, Ocean and Cosmic Rays Vol.5, (2000), 100-103.

[12] KERVALISHVILI G.: Diocotron instability in gas-discharge nonneutral electron plasma, when magnetic field is not parallel to the anode surface, Bulletin of Georgian Academy of Sciences 167, no.3 (Dezember 2002) 442-445